Getting started

This chapter presents all the information the user needs to make the best use of GLOW. Section Geometry Definition provides details about the available functionalities for setting up a geometry layout and displaying it in the 3D viewer of SALOME. Section Lattice Analysis and Export provides information about the process that GLOW automatically performs to generate the output .dat file containing the description of the geometry layout. In both sections, the available functionalities for building and exporting a geometry layout are described with code snippets showing their usage. Images are also provided to graphically present the results displayed in the 3D viewer of SALOME. Lastly, section Usage gives indications about how to include the functionalities of GLOW in a Python script and how to run the script in the SALOME environment.

Geometry Definition

From a topological point of view, the GEOM module of SALOME enables the creation of the following entities:

vertex, which is a point in the XYZ space;

edge, made by two vertices, can be classified as segment, arc of circle or circle;

wire, a closed set of edges;

face, a 2D area made from one or two wires;

shell, made from a group of faces;

solid, a 3D object made from a group of shells;

compound, a container grouping together several GEOM entities.

GLOW relies on most of the above-mentioned topological entities to assemble the geometry layouts and visualize them in the 3D viewer of SALOME. In addition, the specific GEOM functions enabling the operations for building topological entities and applying operations among them are provided in module geom_interface.

In GLOW, a cell, identified by any of the subclasses of Cell, is the base unit of the geometry layout. Cells are built from a characteristic surface, i.e. a subclass of Surface, which represents a GEOM face. Cells can either have a rectangular or an hexagonal shape. Several surfaces can be juxtaposed or overlapped to determine the final layout of a cell by assembling the corresponding GEOM faces together. The construction of a cell geometry layout relies on boolean operations, in particular the partition (function make_partition()) one. This operation cuts one GEOM face with another, and viceversa, grouping both cut faces with the intersected area. The result is a GEOM compound, which represents the geometry layout of a cell, as made of GEOM faces identifying the different areas.

In GLOW, the geometry layout of a cell is described in terms of:

the technological geometry, which is the one delimiting the different cell’s regions in terms of the materials;

the sectorized geometry, which further subdivides the cell’s regions of the technological geometry into sectors.

Lattices, identified by Lattice instances, are made by the repetition of adjacent cells in the 2D space. As for cells, also lattices can be displayed in terms of one of these two types of geometry by accessing the corresponding geometry layout of its cells.

All the areas (i.e. the GEOM faces) of a cell, or a lattice, can be associated with properties, such as the material. In GLOW, these areas are referred to as regions. To enable the visualization of the single GEOM faces (i.e. the regions) constituing a cell, or a lattice, with a specific colorset for a type of property, GLOW relies on instances of the dataclass Region. Each instance associates any of the GEOM face of the geometry layout (either technologial or sectorized) with a color corresponding to the value of the property type to be visualized in the SALOME 3D viewer.

The three main classes that are involved in the definition of the geometry layout of a cell or a lattice are Surface, Cell and Lattice. A Surface represents a single GEOM face, while Cell and Lattice are identified by a GEOM compound. Surfaces are intended to facilitate the definition of the GEOM compound that defines the technological geometry of the cell. Conversely, the sectorized geometry and the associated GEOM compound are defined by acting on the technological geometry using methods from the Cell and Lattice classes. Surface, Cell and Lattice classes rely on the same functionalities that apply transformation and visualization operations. Here, transformation refers to rotating and translating the geometric object in the XYZ space, and visualization refers to displaying the object in the 3D viewer of SALOME. Each of the aforementioned classes provides its own implementation of these operations.

In the following, the three main classes describing surfaces, cells and lattices are discussed and their public methods are detailed.

Surfaces Definition

GLOW comes with classes to quickly build specific surfaces, identified by GEOM faces, in SALOME. In the Object-Oriented Programming (OOP) view, the types of surface that are available in GLOW inherit from the same superclass Surface, which is an abstract class characterised by both abstract and concrete methods. The classes to build specific surfaces are the following:

class Circle that addresses circular surfaces.

class Hexagon that addresses hexagonal surfaces.

class Rectangle that addresses rectangular surfaces.

class GenericSurface that addresses any 2D surface created in SALOME.

Depending on the specific type of surface, the instantiation requires to specify the centre of the surface and its characteristic dimensions (i.e. radius for a circle, width and height for a rectangle, the edge length for a hexagon). Classes are implemented with default values for the characteristic dimensions. When an object of the Surface subclasses is instantiated, the GEOM objects for the vertices, the edges and the corresponding face are automatically built. In this way, the surface can be shown in the SALOME 3D viewer right after the initialization by means of the method show_face().

The following code snippet shows how to instantiate and display a geometric surface for a hexagonal case.

from glow.geometry_layouts.geometries import Hexagon

surface = Hexagon(center=(1.0, 1.0, 0.0), edge_length=2.0)
surface.show_face()

Fig. 1 shows the graphical result obtained by running the code above in a Python script or directly from the Python console of SALOME.

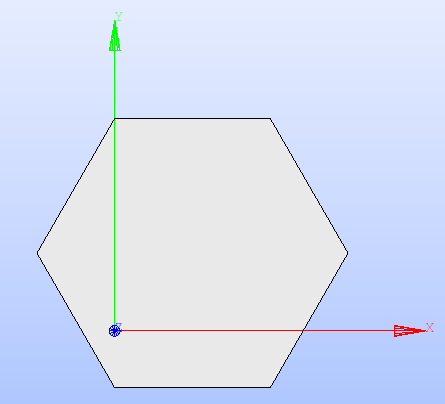
Hexagon in SALOME — Fig. 1 Hexagon displayed in the *SALOME* 3D viewer.

Transformation operations can be applied by calling the methods for rotating or translating the surface, which are declared in the base class Surface, and are accessible for any of its subclasses. The method rotate() performs a rotation of the GEOM elements of Surface around the centre of the corresponding GEOM face by a given rotation angle, in degrees. The direction of the rotation follows the standard right-hand rule. The method translate() moves the GEOM elements of Surface so that the center of the corresponding GEOM face coincides with the given XYZ coordinates. For the hexagonal surface declared above, the code instructions are the following:

surface.rotate(90)
surface.translate((0.0, 0.0, 0.0))
surface.show_face()

By applying these methods, the resulting GEOM face is shown in Fig. 2.

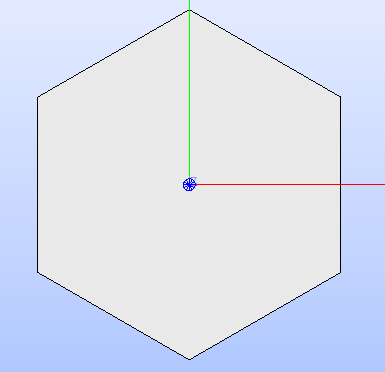
Hexagon rotated and translated in SALOME — Fig. 2 Hexagon after applying rotation and traslation operations, as shown in the *SALOME* 3D viewer.

The GEOM face that is specific of the subclass of Surface can be directly modified within SALOME and the modified GEOM face applied to the Surface object by calling the method update_from_face(). The implementation of this method is specific for each of the subclasses of Surface. In general, the method receives as parameter a GEOM face and updates the instance attributes of Surface accordingly. A check ensures that only GEOM faces are provided, and that the given GEOM face corresponds to the characteristic surface the Surface class refers to.

Cell Definition

GLOW comes with classes to build cells having either a hexagonal or a rectangular characteristic surface. The module glow.geometry_layouts.cells provides the abstract base class Cell, which represents a cell described in terms of an instance from the subclasses of the Surface base class. The subclasses of Cell are the following ones:

class RectCell that represents rectangular cells.

class HexCell that represents hexagonal cells.

class GenericCell that represents cells characterised by any GEOM face or GEOM compound created in SALOME.

When instantiating any of the aforementioned sublasses, the corresponding instance of the Surface subclasses is built. Depending on the cell type, the instantiation requires either the characteristic dimensions of the surface (e.g. width and height for a rectangle or edge length for a hexagon) or the GEOM face, or GEOM compound, directly (GenericCell case).

The following code snippet shows how to instantiate the different type of cells available in GLOW.

from glow.geometry_layouts.cells import GenericCell, HexCell, RectCell

hex_cell = HexCell(
    center=(0.0, 0.0, 0.0),
    edge_length=1.0,
    name='HexCell')

rect_cell = RectCell(
    center=(0.0, 0.0, 0.0),
    height_x_width=(1.0, 2.0),
    rounded_corners=[(1, 0.1), (3, 0.1)],
    name='RectCell')

gnrc_cell = GenericCell(shape=surface)

For a rectangular cell, the rounded_corners parameter indicates the index of the corner of the rectangle and the associated curvature radius to generate a rectangle with rounded corners. For a GenericCell, the instantiation requires to specify a GEOM face or a GEOM compound representing its geometric surface.

The class Cell declares attributes and methods common to all its subclasses. Public methods cover the following functionalities:

displaying the cell’s geometry layout in the SALOME 3D viewer;

adding and removing circles within the cell’s boundaries;

applying transformation operations for rotating and translating the cell’s characteristic GEOM elements;

applying a sectorization operation of the cell’s geometry layout;

setting up values for the available property types associated to one or all the regions of the cell’s technological geometry;

inspecting the information (name and properties value) related to a specific region of the cell that has been selected in the SALOME 3D viewer;

updating the cell’s geometry layout with a GEOM face or a GEOM compound;

restoring the cell to its original state in terms of both geometry and the properties associated with its regions.

In the following, all these methods are detailed.

Displaying the Cell’s Geometry Layout

The cell’s geometry layout can be displayed in the SALOME 3D viewer by calling the method show(). The method has two parameters, each associated with a default value:

property_type_to_show, an item of the enumeration PropertyType, it identifies the property type (e.g. the material) according to which the cell’s regions (i.e. the GEOM faces) are displayed with a color. Each region has a colour associated with the value of the indicated property type. If no property type is provided, the regions are displayed with a default colour.

geometry_type_to_show, an item of the enumeration GeometryType, it identifies the type of geometry to show, i.e. either the technological or the sectorized one. The cell’s regions, identified by a list of objects of the dataclass Region, are build from the GEOM compound associated with the technological or sectorized layout. By default, the method displays the regions of the technological geometry.

Users should note that the method show() will raise an exception if they request to display the regions according to a property type for which a region has no corresponding value.

The following code snippet shows how to display the regions of the cell’s technological geometry (indicated by the TECHNOLOGICAL type of geometry) with a colorset in terms of the property type MATERIAL.

hex_cell.show(
    property_type_to_show=PropertyType.MATERIAL,
    geometry_type_to_show=GeometryType.TECHNOLOGICAL
)

Regions are added to the Object Browser in SALOME as children of the cell they belong to. If not displayed automatically (it can happen when running a new SALOME instance with a script), they can be shown by selecting the “Show Only Children” item in the contextual menu for the cell (see Fig. 3).

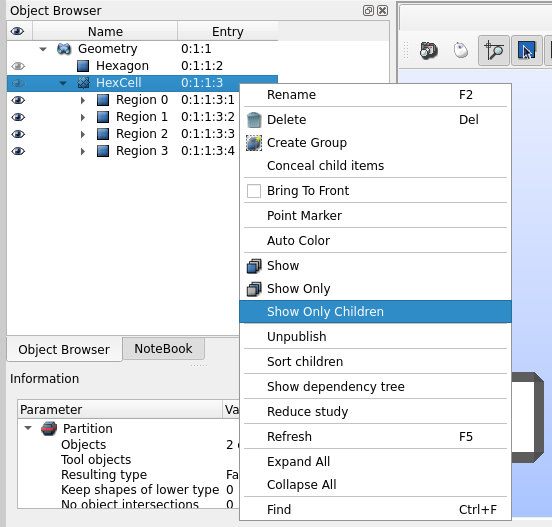
How to display the cell's regions in SALOME — Fig. 3 How to display the *regions* associated to a cell in *SALOME*.

The geometry layout resulting from the aforementioned code is shown in Fig. 4.

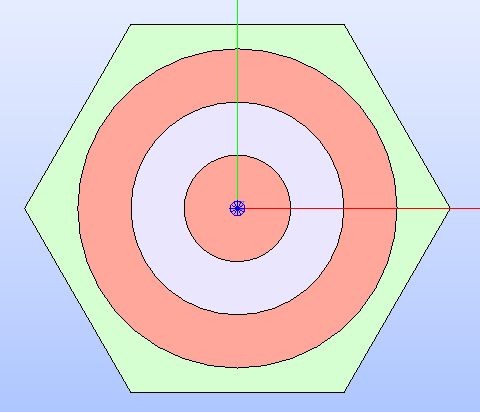
Cell's technological geometry with MATERIAL colorset — Fig. 4 Hexagonal cell’s technological geometry with the `MATERIAL` colorset.

Circles Addition and Removal

Typically, fuel pin cells, having either a cartesian or a hexagonal geometry, are characterised by several concentric circles to represent the different regions of a cell, each having its own properties. In general, circles can be placed either in the cell’s centre or in any other point within its boundaries.

In GLOW, the method add_circle() allows to position a circle, with a specified radius, inside the cell. The addition is performed only if the circle’s radius does not exceeds the characteristic dimensions (e.g. the apothem for a hexagon) of the surface ( Surface subclasses) the cell is based on. Given the circle’s radius, a GEOM face object is built in the given position, if any is specified, otherwise the circle is added in the cell’s centre. In any case, a partition operation between the GEOM compound representing the current technological geometry of the cell and the GEOM face of the new circle is performed, resulting in a GEOM compound that comprises both.

The following code snippet shows how to add circles in specific positions within a hexagonal cell.

hex_cell.add_circle(radius=0.5)
hex_cell.add_circle(radius=0.1, position=(0.2, 0.2, 0.0))
hex_cell.show()

Fig. 5 shows the result of adding two circles, the first in the cell’s centre, the second in a specific position. The resulting updated technological geometry is shown in the SALOME 3D viewer after calling the method show().

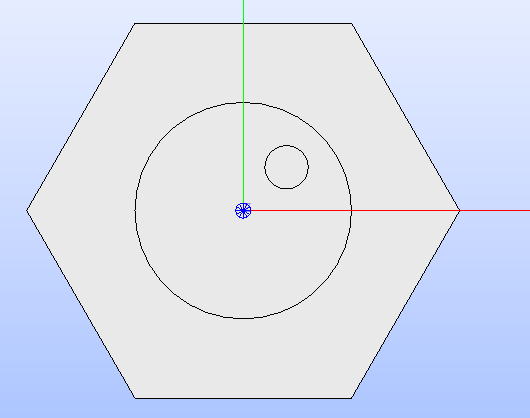
Hexagonal cell with two circular regions in SALOME — Fig. 5 Hexagonal cell’s geometry layout after adding two circles to its technological geometry.

Calling the method add_circle() updates the technological geometry of the cell. The same goes for the method remove_circle().

When any property type (e.g. a material) has been assigned to the cell’s region where the circle is added, the regions resulting from partitioning the cell with the circle inherit the properties of the overlapped regions (see Fig. 6).

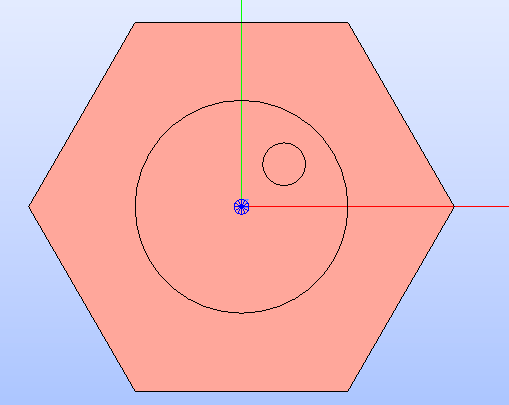
Hexagonal cell with property colorset in SALOME — Fig. 6 Hexagonal cell’s technological geometry shown with a properties colorset; the new circular *regions* have the same property type value as the *region* they overlap.

If the added circle is cell-centred, then it also inherits the sectorization options of the overlapped centred region (see Fig. 7).

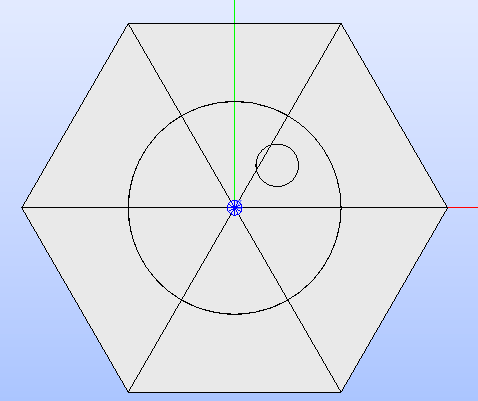
Hexagonal cell with sectorization visualization in SALOME — Fig. 7 Hexagonal cell’s sectorized geometry; only the cell-centred circle is subdivided in six regions as the the overlapped *region*.

When removing a circular region having any property type or sectorization option associated, the region resulting from its removal keeps the same values of the region that surrounded the removed circular region.

Transformation Operations

Transformation operations can be applied by calling the methods for rotating or translating the cell’s geometric elements, i.e. the GEOM compounds representing the cell’s technological and sectorized layouts, as well as the Region objects corresponding to the layout currently displayed. The method rotate() requires the rotation angle, in degrees, and assumes that the rotation is performed around the Z-axis. The direction of the rotation follows the standard right-hand rule. The method translate() needs the XYZ coordinates of the new centre of the cell. While the former operates on the same instance, the latter returns a deep copy of the original instance positioned in the new centre. For a hexagonal cell, the code instructions for rotating and translating the cell are the following:

hex_cell.rotate(90)
new_cell = hex_cell.translate((1.0, 1.0, 0.0))
new_cell.show()

Sectorization Operation

Other than the technological geometry, cells can be displayed also in terms of the sectorized one. This type of geometry consists in subdividing the cell’s regions of the technological geometry in a number of angular regions (the sectors) which is specific for the type of cell. Subclasses of Cell declares the available number of sectors a region of the technological geometry can have, as well as the starting angle from which the subdivision starts. We can have the following values:

HexCell - admitted number of sectors are either 1 or 6, while 0 or 30 for the starting angle.

RectCell - admitted number of sectors are 1, 4, 8 and 16, while the corresponding angles are 0 and 45.0 for a subdivision in four sectors, 0 and 22.5 for a subdivision in eight sectors, 0 for a subdivision in one or sixteen sectors.

Rectangular cells also have the option of applying a windmill sectorization to the region farthest from the cell’s center, provided that the region is subdivided into eight sectors.

Each of the subclasses of Cell provide their own configuration for applying the sectorization. In particular, for a RectCell the windmill parameter can be provided to apply a windmill sectorization, while for HexCell and GenericCell this parameter is absent. In any case, the logic for subdividing the regions in sectors is common to all subclasses.

The following code snippet shows how to apply a sectorization, with windmill option enabled, for a cartesian cell having two cell-centred circles.

rect_cell.sectorize([1, 4, 8], [0, 45, 22.5], windmill=True)
rect_cell.show(geometry_type_to_show=GeometryType.SECTORIZED)

Elements in the two lists provided to the method sectorize() are associated to the regions from the closest to the farthest one from the cell’s centre. Fig. 8 shows the result after applying the indicated sectorization.

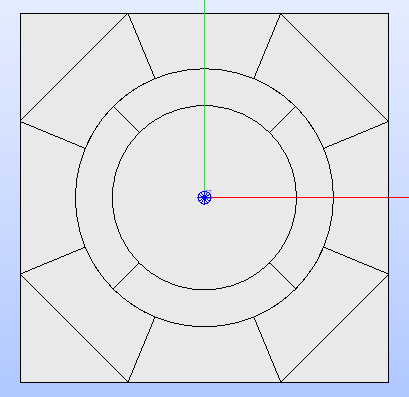
Cartesian cell after its sectorization — Fig. 8 Cartesian cell after applying the sectorization operation. The number of subdivisions of the cell’s *regions* matches the order in which sectorization numbers are provided to the method.

Setting Up the Cell’s Regions Properties

Cells’ regions can be displayed by applying a colorset that depends on the type of property to show, as item of the PropertyType enumeration. An example of property type is the material constituing each region, identified by the item MATERIAL. To set values for a specific property type, users can rely on two methods:

set_properties(), which allows users to set values for different types of properties for all the regions of the cell’s technological geometry. The convention for declaring the values of a property is from the closest to the farthest region with respect to the cell’s centre.

set_region_property(), which allows to set a value for the indicated type of property of a single region of a cell; this can be either the GEOM face currently selected in the SALOME 3D viewer or the one provided as parameter to the method.

The following code snippet shows how to apply values for the MATERIAL type of property, which is the only one currently implemented.

rect_cell.set_properties(
    {PropertyType.MATERIAL: ['GAP', 'FUEL', 'COOLANT']}
)
rect_cell.add_circle(0.1)
rect_cell.set_region_property(
    PropertyType.MATERIAL,
    'MAT',
    Circle(radius=0.1).face
)
rect_cell.show(PropertyType.MATERIAL)

In particular, given a cartesian cell with two cell-centred circles, the first method enables all the material values to be set at the same time. A new circular region is added, and the corresponding GEOM face is used to identify the region within the cell to which the property should be assigned. From within the SALOME 3D viewer, the region can be provided by simply selecting the corresponding GEOM face and calling the method from the integrated Python console. In any case, the cell’s geometry layout with the MATERIAL colorset is shown in Fig. 9.

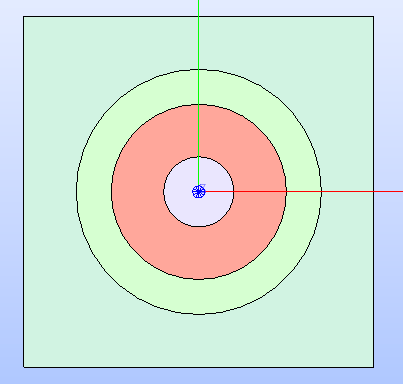
Cartesian cell after setting up the properties — Fig. 9 Cartesian cell after setting up values for the `MATERIAL` property type for each region. It is shown with a colorset highlighting the different values assigned to the cell’s *regions*.

Inspection of Regions

When regions of a cell are displayed in the SALOME 3D viewer, users can obtain information about an individual region, including its assigned properties. This is done by calling the method get_regions_info() directly in the Python console of SALOME from an object of any of the subclasses of Cell. If no region (as GEOM face), or more than one, is selected when calling the method, an exception is raised. The available information, which is printed in the Python console, includes the name of the cell’s region and the value for each of the assigned type of properties (see Fig. 10).

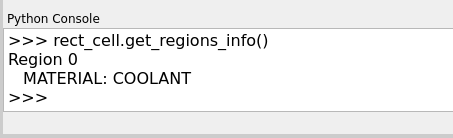
Information about a selected region of the cell — Fig. 10 Information about a selected *region* of the cell; its name and values for the assigned properties are printed.

Updating the Cell’s Geometry Layout

The methods of the class Cell enable the cell’s technological and sectorized geometries to be customized by means of circles and lines, where the latter must follow the rules tied to the sectorization operation (i.e. lines subdivides regions of the technological geometry in fixed numbers of angular sectors). To support any customization of the cell’s geometry layout, while keeping the base surface (subclass of Surface) the same, two methods are provided:

update_geometry(), which enables to update the GEOM compound, representing either the technological or the sectorized geometry, that is displayed in the SALOME 3D viewer with the GEOM face or GEOM compound currently selected.

update_geometry_from_face(), which enables to update the GEOM compound corresponding to the indicated GeometryType with the given GEOM face or GEOM compound.

In both cases, the result is a new layout for the technological or the sectorized geometry where the new regions inherit the already assigned properties, if any; the same goes for the sectorization options.

The following code snippet shows how the cell’s technological geometry could be updated with a non-standard geometry built by overlapping two hexagonal surfaces with different dimensions.

hex_1 = Hexagon(edge_length=1)
hex_2 = Hexagon(edge_length=1.5)

shape = make_partition([hex_2.face], [hex_1.face], ShapeType.COMPOUND)

hex_cell = HexCell()
hex_cell.update_geometry_from_face(GeometryType.TECHNOLOGICAL, shape)
hex_cell.show()

The function make_partition() cuts a list of GEOM faces (in the first argument) with those provided in the list as second argument; the resulting type of shape is indicated as third argument. After applying the built geometry to the cell, the result can be displayed in the SALOME 3D viewer (see Fig. 11).

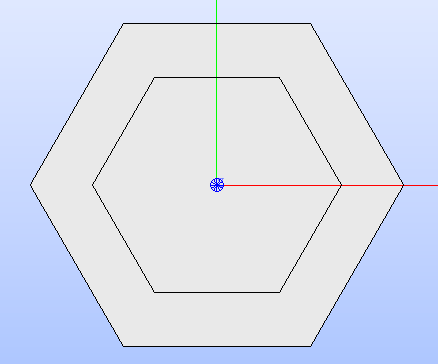
Cell's geometry after update — Fig. 11 Hexagonal cell’s layout after updating its technological geometry.

Restoring Cell’s State

There could be cases where users need to reset the cell’s geometry layout and the properties associated to its regions (see Hexagonal Assembly With Different Cells). The method restore() satisfies this need by restoring the GEOM compound of the cell’s technological layout to its base surface (e.g. a GEOM face identifying a rectangle) without any inner circle. The sectorized layout, as well as the properties and sectorization options, are completely removed.

Lattice Definition

GLOW comes with classes to build lattices characterised by either hexagonal or cartesian cells. The module glow.geometry_layouts.lattices provides the class Lattice to describe any kind of lattice of cells. The type of lattice is determined by the type of the cells, either cartesian or hexagonal. All the cells in the lattice must be of the same type, identified by an item of the enumeration CellType. This is automatically set at instantiation time or when adding cells to the lattice.

The Lattice class can be instantiated either without any cell or by providing a list of objects of the subclasses of Cell.

In GLOW, the logic behind the construction of a lattice relies on the layer concept: when a new cell, or a group of cells is added to the lattice, the cells are associated to a layer (either a new layer or an existing one already containing some cells). The layer to which the cells are added depends on the specific method used to add them. By adopting this logic, GLOW can easily handle the construction of the GEOM compound that identifies the lattice geometry layout, especially in the case of lattices made by superimposing cells with different dimensions.

The following code snippet shows how to instantiate a lattice with the cartesian or hexagonal cells available in GLOW.

from glow.geometry_layouts.cells import HexCell, RectCell
from glow.geometry_layouts.lattices import Lattice

hex_cell = HexCell()
rect_cell = RectCell()

# Lattice instantiation by providing all the cartesian cells at once
cart_lattice = Lattice(
    cells=[
        rect_cell.translate((0.5, 0.5, 0.0)),
        rect_cell.translate((-0.5, 0.5, 0.0)),
        rect_cell.translate((-0.5, -0.5, 0.0)),
        rect_cell.translate((0.5, -0.5, 0.0)),
    ],
    name="Cartesian Lattice",
    center=(0.0, 0.0, 0.0),
    boxes_thick=[0.075, 0.075]
)
# Lattice instantiation without any cell
lattice = Lattice()
# Lattice instantiation with a hexagonal central cell
hex_lattice = Lattice([hex_cell])

The three examples show different instantiations; in particular, we have:

a cartesian lattice built from a list of cells positioned to recreate a 2x2 pattern; by specifying the boxes_thick parameter, the built lattice is enclosed within a rectangular box made by two layers of given thicknesses.

a lattice built without any cell. The lattice’s methods for adding cells need to be called to define its geometry layout (see Adding cell(s)).

a hexagonal lattice built from a single cell positioned in the centre of the lattice.

Similarly to the cells, the two types of geometry layout, the technological and the sectorized ones, apply to the lattice (see Geometry Definition).

The Lattice public methods cover the following functionalities:

building the lattice’s regions, as elements of the dataclass Region, according to either the technological or the sectorized type of geometry of the cells in the lattice;

displaying the lattice’s geometry layout in the SALOME 3D viewer;

adding a single cell or a group of the same cell organised in one or more rings around the lattice’s centre;

transformation operations for rotating or translating the lattice’s cells;

enclosing the lattice in a box declared from the thicknesses of its layers or by means of an instance of the subclasses of Cell;

setting up the properties associated to one region of the lattice or to the ones of the box;

applying a specific type of symmetry in accordance with the type of lattice;

setting the type of geometry in accordance with the type of lattice and of applied symmetry;

inspecting the information related to a specific region of the lattice that has been selected in the SALOME 3D viewer;

restoring a list of cells of the lattice to their original state, both in terms of geometry and properties.

Building Lattice’s Regions

To facilitate displaying and exporting the lattice’s geometry layout, the method build_regions() is provided. It builds a list of Region objects that are representative of the regions in which the lattice is subdivided when assembling all the cells together with the box, if present. Cells can be associated with different layers of cells in the lattice. When the lattice’s regions are built to be displayed in the SALOME 3D viewer, a process is carried out. This can be imagined as if all the layers were collapsed into a single layer of cells. The layers are traversed from top to bottom, and any cells that are found to be overlapped by those of a higher layer are either cut or removed from the lattice. Fig. 12 shows the result of overlapping a cell with others.

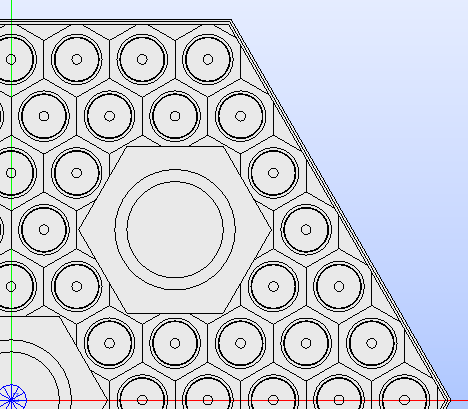
Lattice with a cell overlapping other cells — Fig. 12 Hexagonal lattice where a cell overlaps other cells of an inferior layer.

If any symmetry is applied or the lattice is enclosed in a box, the GEOM compound of the assembled cells is either cut to extract the portion that replicates the symmetry or assembled with the geometry layout of the box. Given the final GEOM compound, the contained GEOM faces are extracted and a Region object is built for each one. In any case, the property assignment involves identifying the corresponding region among the ones of the technological geometry of the lattice’s cells.

According to the type of geometry of the cells that is provided to the method build_regions(), the resulting regions describe either the technological or the sectorized geometry of the lattice.

Displaying the Lattice’s Geometry Layout

The lattice’s geometry layout can be displayed in the SALOME 3D viewer by calling the method show(). Depending on its parameters, it builds and displays the corresponding regions (i.e. the GEOM faces) of the lattice.

Regions are built and shown according to either the technological or the sectorized geometry by specifying it as parameter of the method. The same considerations on the parameters done for the method show() of the subclasses of Cell are valid for the lattice as well (see Displaying the Cell’s Geometry Layout). It is important to note that when displaying the lattice’s regions with a colorset according to the indicated PropertyType, regions with the same property type value are coloured the same.

In SALOME, regions are added to the Object Browser as children of the lattice they belong to, similarly to what happens for cells (see Fig. 3).

The following code snippet shows how to display the regions of the lattice’s technological geometry (indicated by the TECHNOLOGICAL type of geometry) with a colorset in terms of the property type MATERIAL.

cart_lattice.show(
    property_type_to_show=PropertyType.MATERIAL,
    geometry_type_to_show=GeometryType.TECHNOLOGICAL
)

Fig. 13 shows the resulting geometry layout of the lattice after running the above code.

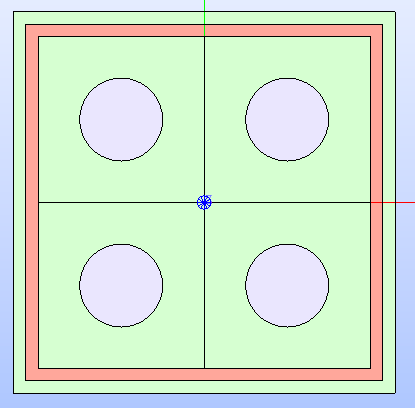
Lattice's technological geometry with the MATERIAL colorset — Fig. 13 Cartesian lattice’s technological geometry with the `MATERIAL` colorset.

Adding cell(s)

A lattice can be built by instantianting a Lattice object, providing a list of Cell subclasses. In addition to this approach, it is often useful to contruct a lattice by adding a cell or a ring of cells with simple methods. For this reason, the following methods have been introduced:

add_cell(), which allows to add a single cell at an indicated position;

add_ring_of_cells(), which allows to add a ring of the same cell at the indicated ring index;

add_rings_of_cells(), which allows to add the indicated number of rings of the same cell, starting from the current ring index occupied by cells.

The method add_cell() adds the cell to the specified position, if any is provided, otherwise the cell is placed at the position indicated by the cell’s centre. It is important to note that any cell added with this method is included in a new layer, i.e. a new sub-list is created for the attribute layers containing the cell itself.

The layout of a lattice can be considered as consisting of several rings, each occupied by an increasing number of cells as the ring index increases. The two methods add_ring_of_cells() and add_rings_of_cells() provide a quick way for adding one or more rings of cells. The former adds the cells at the given ring index while the latter adds the indicated number of rings of cells starting from the maximum value of ring index currently present in the lattice. Users should also note that, while the former method enables them to specify the layer to which the ring of cells is added (by providing its index), the latter always adds the rings of cells to a new layer.

All the aforementioned methods do not allow to mix cells with different types (i.e. having different item of the enumeration CellType); this ensures that all the cells have either a cartesian or a hexagonal type.

The following code snippet shows the different ways to add cells to a lattice.

cell = HexCell()
lattice = Lattice([cell])

lattice.add_ring_of_cells(cell, 1)
lattice.add_rings_of_cells(cell, 2)
lattice.add_cell(cell, (1.5, 1.5, 0.0))
lattice.show()

The lattice’s geometry layout resulting from adding hexagonal cells using the three methods is shown in Fig. 14.

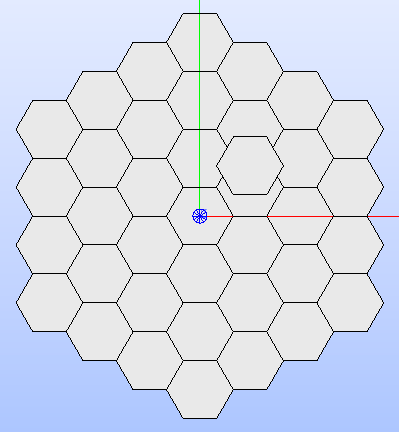
Lattice after adding cells — Fig. 14 Hexagonal lattice built by applying the three methods for adding cells.

Lattice’s Transformation Operations

Transformation operations can be applied by calling the methods for rotating or translating the lattice’s geometric elements, i.e. the GEOM compound objects representing its full and partial (if any symmetry is applied) geometry layouts, the contained cells, including the box (if present), and all the regions. The method rotate() requires the rotation angle, in degrees, and assumes that the rotation is performed around the Z-axis. The direction of the rotation follows the standard right-hand rule. The method translate() needs the new XYZ coordinates of the centre of the lattice. Users should note that both methods operate on the same instance and the result of the transformation is directly shown in the SALOME 3D viewer.

Enclosing the Lattice in a Box

In nuclear reactors, fuel assemblies are typically framed in a metallic container. To replicate exactly the same kind of layouts, GLOW allows to insert a lattice within a box. A box is an instance of the subclasses of Cell which can be built either from the thickness of its layers or by instantiating the corresponding Cell object directly. The former case relies on the method build_lattice_box(), which, given the type of lattice (i.e. hexagonal or cartesian), automatically instantiates a Cell object built by overlapping as many rectangles or hexagons as the number of the indicated thicknesses of the layers. If all the values provided to the build_lattice_box() method are positive (independently from the value), the borders of the layer closest to the centre of the lattice touch the outermost ring of cells without overlapping it (see Fig. 15). The method also allows the first thickness value in the list to be negative, which handles a situation where the layer closest to the centre cuts the farthest ring of cells (see Fig. 16).

The following code snippet shows how to build a box for the lattice using the method build_lattice_box() with the thickness of the first layer either being positive or negative.

lattice.build_lattice_box([0.1, 0.1])
lattice.show()

lattice.build_lattice_box([-0.1, 0.1])
lattice.show()

The result of applying both method calls separately, for a hexagonal lattice, is shown in Fig. 15 and in Fig. 16 respectively.

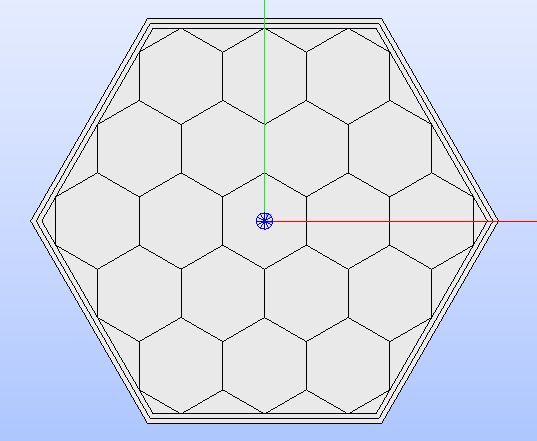
Lattice within a box with positive thicknesses — Fig. 15 Hexagonal lattice framed in a box with all positive thicknesses for the layers.

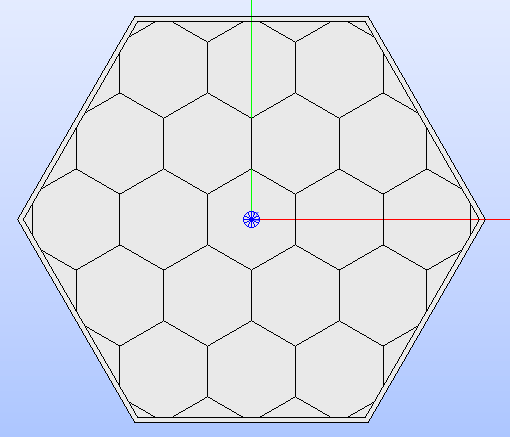
Lattice within a box with negative first thickness — Fig. 16 Hexagonal lattice framed in a box with a negative thickness for the first layer. The box cuts the farthest ring of cells.

The lattice’s box can also be declared by setting the corresponding property lattice_box with an object of the subclasses of Cell. The setter of the property requires the cell’s centre to coincide with that of the lattice, otherwise an exception is raised. Both Cell objects or None are valid inputs for the setter. The latter can be used to remove any box previously set.

Both approaches to setting a box lead to the same result: the GEOM compound representing the geometry layout of the lattice is updated by assembling the GEOM compound of each cell with that of the box, which can potentially cut the GEOM compound of the cells of the farthest ring.

Setting Up Properties

Just like for cells, the regions of a lattice can be displayed with a colorset according to the type of property to display, as item of the PropertyType enumeration.

There are different ways for users to set values for a specific property type of a region of the lattice. If the region belongs to any cell, the methods previously described (see Setting Up the Cell’s Regions Properties) for a Cell object remain valid, provided they are applied to the correct instance stored in the attribute layers.

In addition, users can rely on the following methods of the class Lattice:

set_region_property(), which allows to set a value for the indicated type of property of a single lattice’s region (i.e. a GEOM face); this can be either the GEOM face currently selected in the SALOME 3D viewer or the one provided as parameter to the method.

set_lattice_box_properties(), which allows users to set values for different types of properties for all the regions of the Cell instance, which is the box that encloses the lattice. The convention for declaring the values of a property is always the same, i.e. from the region closest to the center to the farthest region. Users should note that for hexagonal boxes, the number of values to provide is always equal to that of the layers plus one. The reason is that the first value in the list is associated with the regions between the cells and the first layer of the box. These regions all share the same property type value.

The following code snippet shows the different ways to apply values for the MATERIAL property type, i.e. either to all the cells or to an indicated region or to the regions of the lattice’s box.

# Build the lattice geometry layout
hex_cell = HexCell()
hex_cell.rotate(90)
lattice = Lattice([hex_cell])
lattice.add_ring_of_cells(hex_cell, 1)
lattice.build_lattice_box([0.1])
# The same value for the 'MATERIAL' property is assigned to all the cells
for layer in lattice.layers:
    for cell in layer:
        cell.set_properties(
            {PropertyType.MATERIAL: ['COOLANT']}
        )
# A different value for the 'MATERIAL' property is assigned to the central
# cell
lattice.set_region_property(PropertyType.MATERIAL, 'GAP', hex_cell.face)
# Values for the 'MATERIAL' property are assigned to the box's regions
lattice.set_lattice_box_properties(
    {PropertyType.MATERIAL: ['COOLANT', 'METAL']}
)
lattice.show(PropertyType.MATERIAL)

The resulting lattice’s geometry layout with the MATERIAL colorset is shown in Fig. 17.

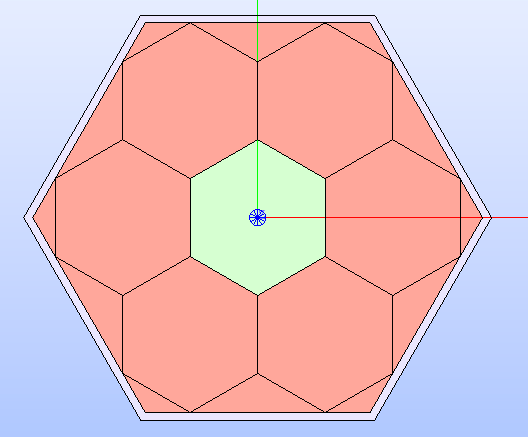
Lattice after setting up the properties — Fig. 17 Lattice after setting up the values for a type of property. It is shown with the corresponding colorset.

Applying Symmetries

Solving the Boltzmann transport equation on the full geometry layout of a fuel assembly can be computationally expensive, in particular if the geometry contains many rings of cells. To speed up the calculations, users can rely on cuts to extract parts out of the existing layout, thereby isolating the minimum portion of the geometry required to describe the entire pattern. GLOW supports the application of specific types of symmetries to the lattice. According to the type of cells in the lattice, we can have:

Half, quarter, and eighth symmetries for a cartesian lattice. Half and quarter symmetries cut out the corresponding rectangular portion of the lattice, while the eighth symmetry cuts out a right triangular portion with a centre angle of 45°.

Third, sixth and twelfth symmetries for a hexagonal lattice framed in a box. The third symmetry cuts out a parallelogram of the lattice, the sixth symmetry a regular triangle and the twelfth a right triangle with a centre angle of 30°.

The method apply_symmetry() allows users to apply the indicated type of symmetry as item of the enumeration SymmetryType. Since GLOW considers that only specific types of symmetry are allowed for each type of lattice, an exception is raised if the user tries to apply an invalid symmetry. Independently from the type of symmetry, the method apply_symmetry() automatically performs cut operations on the GEOM compound of the lattice so that the remaining part describes the requested symmetry.

For cartesian lattices, the operation of applying a symmetry is performed independently of the presence of a box. However, for hexagonal lattices, GLOW requires the lattice to be framed in a box. This is because the SALT module of DRAGON5 cannot track the resulting geometry layout if the shape is not triangular or quadrilateral.

The following code snippet shows different applications of a symmetry type for a cartesian and a hexagonal lattice.

rect_lattice.apply_symmetry(SymmetryType.QUARTER)
hex_lattice.apply_symmetry(SymmetryType.TWELFTH)

When calling the method apply_symmetry(), the geometry layout of the lattice is automatically updated and displayed in the SALOME 3D viewer (if the method is called from its Python console). If the FULL is provided to the method, any previously applied symmetry is removed and the entire geometry layout of the lattice is displayed.

Fig. 18 and Fig. 19 show the results of applying a QUARTER and a TWELFTH symmetry to a cartesian and a hexagonal lattice, respectively.

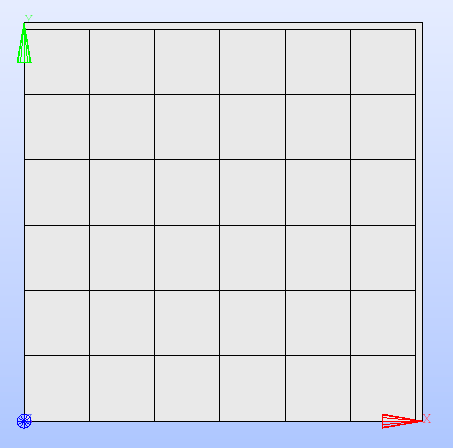
Cartesian lattice after applying a quarter symmetry — Fig. 18 Cartesian lattice after applying the `QUARTER` type of symmetry.

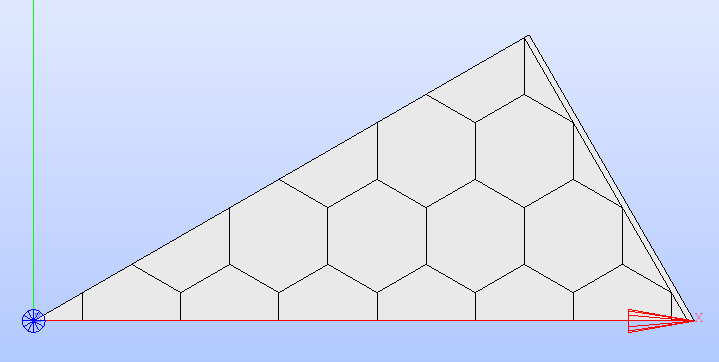
Hexagonal lattice after applying a twelfth symmetry — Fig. 19 Hexagonal lattice after applying the `TWELFTH` type of symmetry.

Users should note that GLOW does not recognize whether the layout of cells replicates the full layout when any valid symmetry is applied. It is up to the user to apply a symmetry that can be representative for the specific layout of the lattice.

Setting the Lattice’s Type of Geometry

The SALT module of DRAGON5 identifies each type of geometry layout of the lattice with a specific index value. In the TDT file, this is identified by the typgeo value which is representative of the geometry layout (either full or partial, if any symmetry is applied) and the type of BCs on the lattice’s borders. User should note that specific values of typgeo are also associated to the two different types of tracking allowed by the SALT module of DRAGON5 [2]. In particular, we have that:

values of 0, 1 and 2 for typgeo are associated with a TISO tracking type, which produces non-cycling tracks distributed uniformally over the domain.

values greater that 2 for typgeo are associated with a TSPC tracking type, which indicates a cyclic tracking over a closed domain.

The items of the enumeration LatticeGeometryType identify the different typgeo values available in GLOW. In particular, we have:

ISOTROPIC to represent a layout having an isotropic reflection on its boundaries. It is associated with a TISO tracking.

SYMMETRIES_TWO to represent a layout having symmetries of two axis of angle pi/n ( \(n>0\)) on its boundaries. It is associated with a TISO tracking.

ROTATION to represent a layout with a rotation of angle 2*pi/n (\(n>1\)) for its boundaries. It is associated with a TISO tracking.

RECTANGLE_TRAN to represent a cartesian layout having a translation BC to its boundaries. It is associated with a TSPC tracking.

RECTANGLE_SYM to represent a full, half and quarter symmetry for a cartesian layout. It is associated with a TSPC tracking.

RECTANGLE_EIGHT to represent a layout with an eighth symmetry. It is associated with a TSPC tracking.

SA60 to represent a layout with an sixth symmetry. It is associated with a TSPC tracking.

HEXAGON_TRAN to represent a full hexagonal layout having a translation BC to its boundaries. It is associated with a TSPC tracking.

RA60 to represent a layout with an sixth symmetry with both rotation and translation BCs to its boundaries. It is associated with a TSPC tracking.

R120 to represent a layout with an third symmetry with both rotation and translation BCs to its boundaries. It is associated with a TSPC tracking.

S30 to represent a layout with a twelfth symmetry. It is associated with a TSPC tracking.

When a Lattice class is instantiated, a default value for the property type_geo is assigned according to the number and the type of cells. Users can assign a value to this property directly, provided it is valid for the lattice’s geometry layout. This means that values specific for a type of lattice and symmetry cannot be applied if not matching the current state of the lattice. For any values of typgeo involving BCs of type translation, the assignement is performed only if the lattice is either made by a single cell or if enclosed in a box.

GLOW provides also the method set_type_geo() to set the item of the enumeration LatticeGeometryType.

The following code snippet shows different applications of the property type_geo.

rect_lattice.type_geo = LatticeGeometryType.RECTANGLE_TRAN
hex_lattice.set_type_geo(LatticeGeometryType.SA60)

Setting the value for the property does not result in any change in the lattice’s geometry layout. It influences the information written in the output TDT file in terms of the BCs section, as this is strictly related to the typgeo.

Lattice’s Regions Inspection

When the regions of the lattice’s technological or sectorized geometry are displayed in the SALOME 3D viewer, information about a selected region, including the assigned properties, can be inspected. The method get_regions_info() can be called directly in the Python console of SALOME from an object of Lattice. If no region (i.e. a GEOM face), or more than one, is selected when calling the method, an exception is raised. The available information, that is printed in the Python console, includes the name of the lattice’s region and the value for each of the assigned type of properties.

Restoring Lattice’s Cells

Similarly to the class Cell, also the class Lattice offers a restore functionality. The method restore_cells() allows users to restore the geometry layout of a group of cells of the lattice by calling the method restore() for each cell. The result is that any circular region of the cells is removed, while also setting the cell’s properties accordingly with the ones passed as input to the method. If any cells have no centered circular regions, the restore operation is not performed for those specific cells. In addition, users can specify whether the operation should be ignored for cells whose circular regions (being part of the technological geometry) have not been cut when overlapping with another cell (see Fig. 12).

This method can be combined with the function get_changed_cells() to retrieve any cells whose geometry layout has been modified, making it easy to restore them.

The following code snippet shows the case of a hexagonal lattice where a central cell overlaps those of the layer below it. The restore operation is applied to all the overlapped cells resulting in the lattice’s geometry layout of Fig. 20.

# Build the lattice geometry layout
cell = HexCell()
cell.add_circle(0.2)
cell.add_circle(0.3)
cell.add_circle(0.4)
cell.rotate(90)
cell.set_properties({PropertyType.MATERIAL: ['MAT_1', 'MAT_2', 'MAT_3', 'MAT_4']})
lattice = Lattice([])
lattice.add_ring_of_cells(cell, 2)
# A cell with greater dimensions is added in the lattice centre, overlapping
# those of the layer below
central_cell = HexCell(edge_length=1.5)
central_cell.rotate(90)
central_cell.set_properties({PropertyType.MATERIAL: ['MAT_4']})
lattice.add_cell(central_cell, ())
# Assemble all the layers
lattice.build_regions()
# Restore the overlapped cells
lattice.restore_cells(
    get_changed_cells(lattice),
    {PropertyType.MATERIAL: 'MAT_4'},
    ignore_not_cut=False
)
lattice.show(PropertyType.MATERIAL)

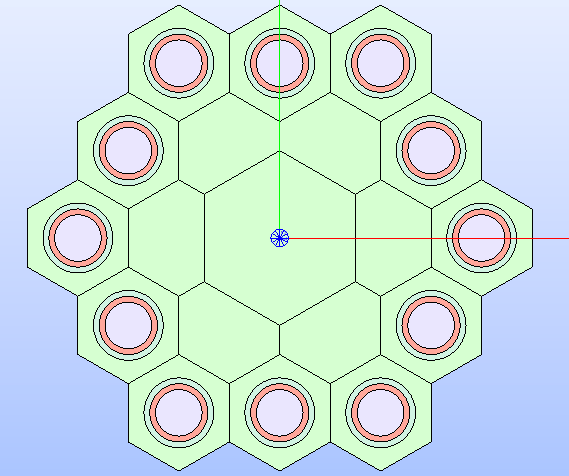
Lattice's after restoring overlapped cells shown with MATERIAL colorset — Fig. 20 Hexagonal lattice’s technological geometry showing the result of restoring the overlapped cells. The geometry layout is displayed with the `MATERIAL` colorset.

Lattice Analysis and Export

The aim of GLOW is to provide neutronics code users with a tool that allows them to create geometry layouts and export the surface geometry representation to a file. This file can then be used to perform a tracking with the SALT module of DRAGON5. The generated file is in the format APOLLO2 requires for its TDT solver.

To meet this requirement, GLOW comes with a functionality for extracting the necessary information about the geometry and generate the output file in the required format.

Once the geometry layout has been created using one or more Lattice instances, users can run the export process by calling the function analyse_and_generate_tdt(). This function first analyses the provided list of lattices with respect to the compound layout representing a portion of them, if any is provided, then generates the output file containing the extracted information.

This function operates on the provided list of Lattice instances on the basis of specific configuration options defined in the dataclass TdtSetup. Values for these options influence the data about the surface geometry representation of the layout contained in the output TDT file, but only if a portion of the entire geometry layout is provided. The available settings in the TdtSetup instance include:

the type of geometry layout of the lattice’s cells, as item of the enumeration GeometryType. A value different from that used to display the lattice in the SALOME 3D viewer can be specified.

the type of property associated to the lattice’s regions, as item of the enumeration PropertyType. A value different to that used to apply the colorset to the regions can be specified.

the value of the albedo, indicating how much reflective the BCs are, i.e. the ratio of exiting to entering neutrons. This attribute can assume values between 0.0 (no reflection) and 1.0 (full reflection) for a ISOTROPIC type of geometry of the lattice. If nothing is provided, a default value that corresponds to the lattice’s geometry type is adopted (i.e. 1.0 for ISOTROPIC geometry layouts, 0.0 for the others). An exception is raised if users provide a value different from 0.0 for a geometry type other than ISOTROPIC, as this would not make sense.

the value for the typegeo parameter, which is strictly related to the type of cells, the applied symmetry and the type of tracking;

the type of symmetry applied to the geometry layout.

The analysis step involves the extraction of the geometric data, that is needed for the generation of the output TDT file, from the layout. The first step consists in determining the GEOM compound to analyse, if one or more lattices are provided; this compound is selected on the basis of the GeometryType and on the applied SymmetryType. In case a GEOM compound is directly provided, it will be used for extracting the geometric data, provided that the GEOM compound is a portion of the given lattice(s). For each Region object, which corresponds to the regions of the layout’s compound, a Face<glow.generator.geom_extractor.Face> object is built and associated with the property type value (PropertyType) for which the layout is analysed. In addition, an index is assigned to ensure their identification. The GEOM edge objects are then extracted and associated to the corresponding regions. This means that each edge, identified with another index, has one or two regions associated with it. Those associated with two regions are internal edges, shared by two adjacent regions, while those associated with only one region are border edges. Lastly, the indices of the border edges are associated to a boundary, whose type (as item of the enumeration BoundaryType) and geometric data are determined on the basis of the LatticeGeometryType and the applied SymmetryType.

Table 1 provides the association between LatticeGeometryType and BoundaryType for the two type of cells with the symmetries available in GLOW. The first group of coloumns LatticeGeometryType-BoundaryType indicates the values for which a uniform tracking (i.e. TISO) should be performed in SALT; the second group refers to values which correspond to a cyclic tracking (i.e. TSPC). An ISOTROPIC type of geometry does not correspond to any BC, whereas those having two types of BCs applies a ROTATION on the internal boundaries and a TRANSLATION on the external ones (see Fig. 21).

Table 1 Available combinations for *TISO* and *TSPC* cases.
CellType	SymmetryType	LatticeGeometryType	BoundaryType	LatticeGeometryType	BoundaryType
HEX	FULL	ISOTROPIC	/	HEXAGON_TRAN	TRANSLATION
	THIRD	ROTATION	TRANSLATION/ROTATION	R120	TRANSLATION/ROTATION
	SIXTH	SYMMETRIES_TWO	AXIAL_SYMMETRY	SA60	AXIAL_SYMMETRY
	SIXTH	ROTATION	TRANSLATION/ROTATION	RA60	TRANSLATION/ROTATION
	TWELFTH	SYMMETRIES_TWO	AXIAL_SYMMETRY	S30	AXIAL_SYMMETRY
RECT	FULL	ISOTROPIC	/	RECTANGLE_TRAN	TRANSLATION
	FULL	ISOTROPIC	/	RECTANGLE_SYM	AXIAL_SYMMETRY
	HALF	SYMMETRIES_TWO	AXIAL_SYMMETRY	RECTANGLE_SYM	AXIAL_SYMMETRY
	QUARTER	SYMMETRIES_TWO	AXIAL_SYMMETRY	RECTANGLE_SYM	AXIAL_SYMMETRY
	EIGHTH	SYMMETRIES_TWO	AXIAL_SYMMETRY	RECTANGLE_EIGHTH	AXIAL_SYMMETRY

The different values of BCs that are automatically applied by GLOW to the boundaries of the lattice’s geometry layout are identified by the items of the enumeration BoundaryType. Their meaning and usage is the same as specified in [2]:

VOID, indicating that boundaries have zero re-entrant angular flux;

REFL, indicating a reflective boundary condition;

TRANSLATION, indicating that the analysed layout is connected to another one for all its boundaries, thus treating an infinite geometry with translation symmetry;

ROTATION, indicating a rotation symmetry;

AXIAL_SYMMETRY, indicating a reflection symmetry;

CENTRAL_SYMMETRY, indicating a mirror reflective boundary condition.

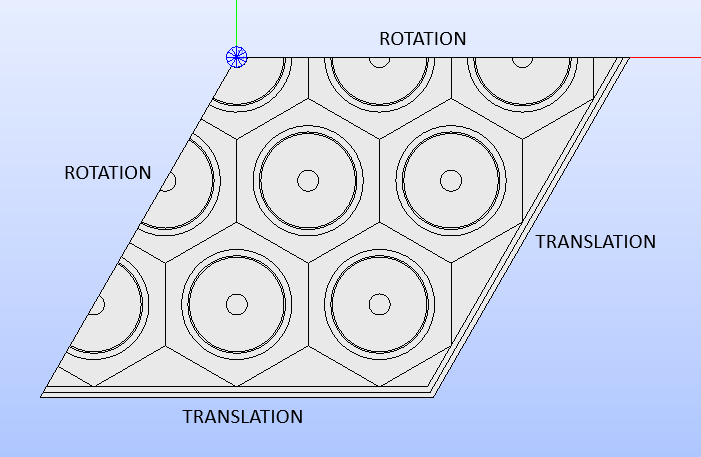
Assignment of ROTATION and TRANSLATION BC types to boundaries — Fig. 21 Showing to which boundaries the `ROTATION` and `TRANSLATION` BC types are assigned to (third symmetry case).

Given all the geometric data extracted from the lattice, the output file is generated. Its structure consists of five sections, that are:

the header section, providing information about the type of geometry (typgeo value), the number of folds (nbfold value), which is consistent with the typgeo, the number of nodes (i.e. the regions), the number of elements (i.e. the edges).

the regions section, providing a list of indices attributed to the regions in the lattice. It also contains the definition of the macros to indicate subvolumes of the assembly.

the edges section, providing the geometric information about all the edges in the geometry layout, as well as the indices of the regions they belong to.

the boundary conditions section, providing information about the BC types and the indices of the edges belonging to each boundary.

the property section, indicating the index of each value of the considered property type (e.g. the MATERIAL one). The order in which values are present matches the indices of the regions.

Usage

GLOW can be used directly by writing down a Python script where the single needed modules can be imported; alternatively, users can import all the modules at once to have them available by setting the following import instruction:

from glow import *

Given that, classes and methods are directly accessible and users can exploit them to:

assemble the geometry;
assign properties to regions;
visualize the result in the SALOME 3D viewer;
perform the geometry analysis and the output file generation.

To run this script, users can:

provide it as argument when running SALOME;
salome my_script.py
load it directly from within the SALOME application.

In addition, since SALOME comes with an embedded Python console, users can import the GLOW modules and exploit its functionalities directly.

To see some of the GLOW functionalities in action, please refer to the script files present in the tutorials folder and described in the Tutorials section. These examples are intended to show a few case studies and how they are managed in GLOW. For further information about the available classes and methods, please refer to the API guide section.