Tutorials

To fully exploit the functionalities offered by GLOW, several examples are provided. They can be found in the tutorials folder. In the following, they are presented and explained in detail, showing for each the resulting geometry layout as displayed in the 3D viewer of SALOME.

Hexagonal Cell

The use case hexagonal_cell.py shows the steps required to declare a single hexagonal cell and customize its geometry layout.

The goal is to instantiate a hexagonal cell whose edge is 1.0 long, having three circles to delimit the different regions where each one is attributed to a specific material. The cell’s technological geometry is declared as follows:

# Build the cell's geometry layout by adding three circular regions
cell = HexCell(name="Hexagonal Cell")
radii = [0.25, 0.4, 0.6]
for radius in radii:
      cell.add_circle(radius)
# Show the cell's technological geometry in the SALOME 3D viewer
cell.show()

By calling the method show(), the cell’s technological geometry is shown in the SALOME viewer (see Fig. 22).

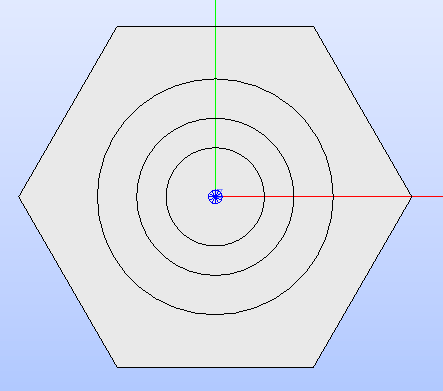
Fig. 22 Hexagonal cell’s technological geometry built by adding three circular regions.

Materials can be assigned to the four regions of the cell’s technological geometry by providing a value for the property type MATERIAL to each. The assignement is performed using the method set_properties(). The names of the materials should be provided in order from the region closest to the cell’s centre to the farthest one. Regions can now be shown with the MATERIAL color map by specifying it in the arguments of the method show() (see Fig. 23).

# Assign the materials to each zone in the cell
cell.set_properties(
    {PropertyType.MATERIAL: ["MAT_1", "MAT_2", "MAT_3", "MAT_4"]}
)
# Show the regions by applying a color map
cell.show(PropertyType.MATERIAL)

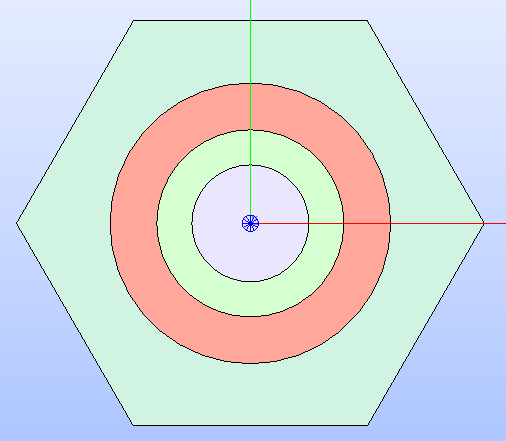
Fig. 23 Hexagonal cell’s technological geometry shown by applying a color map that highlights the type of property MATERIAL applied to the different regions.

Having a refined geometry layout can provide better tracking results; hence, a sectorization can be applied with the method sectorize(). It requires two lists, one with the number of sectors that each region is subdivided into and one with the angle that each sectorization starts from. The refined geometry can be shown even with the MATERIAL colorset by specifying it among the arguments of the method show() together with the SECTORIZED type of geometry (see Fig. 24).

# Build the cell's sectorized geometry
cell.sectorize([1, 1, 6, 6], [0]*4)
# Show the sectorized cell with regions colored according to the 'MATERIAL'
# property
cell.show(PropertyType.MATERIAL, GeometryType.SECTORIZED)

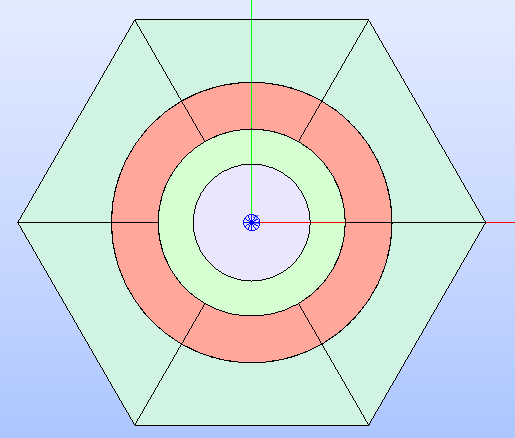
Fig. 24 Hexagonal cell’s sectorized geometry shown by applying a color map that highlights the MATERIAL property type applied to the different regions resulting from the sectorization.

Cartesian Cell With Custom Geometry Layout

The use case cartesian_cell.py shows the steps required to declare a single rectangular cell and customize its geometry layout by means of the functions of the module glow.interface.geom_interface that wrap the ones of the GEOM module of SALOME.

The goal is to instantiate a cartesian cell with a square shape whose edge is 1.0 long. The cell is subdivided into four regions by means of three circles; a specific material is assigned to each of the regions of the resulting technological geometry. The characterization of the cell’s technological geometry follows the same instructions as shown in the previous case. In addition, the MATERIAL property type is assigned to the different regions of the technological geometry of the cell.

# Build the cell's geometry layout by adding three circular regions
cell = RectCell(name="Cartesian cell")
radii = [0.2, 0.3, 0.4]
for radius in radii:
      cell.add_circle(radius)
# Assign the materials to each zone in the cell
cell.set_properties(
    {PropertyType.MATERIAL: ["MAT_1", "MAT_2", "MAT_3", "MAT_4"]}
)

To further refine the geometry layout, a sectorization can be applied with the method sectorize(). In addition to the two lists indicating the number of sectors and the angle the sectorization starts from, a cartesian cell can also receive the boolean flag windmill. This option generates a sectorized geometry where lines are drawn between two successive intersection points between the lines of the sectors and the borders of the cell (see Fig. 25).

# Build the cell's sectorized geometry with 'windimill' option enabled
cell.sectorize([1, 1, 4, 8], [0, 0, 0, 22.5], windmill=True)
# Show the sectorized cell with regions colored according to the 'MATERIAL'
# property
cell.show(PropertyType.MATERIAL, GeometryType.SECTORIZED)

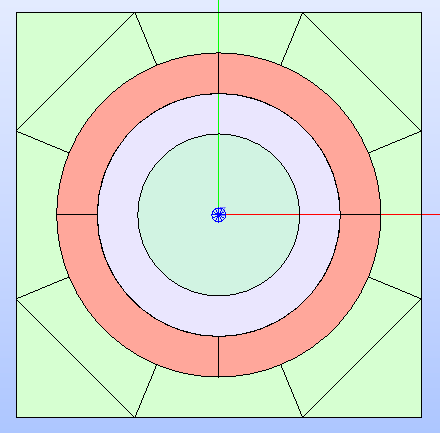
Fig. 25 Cartesian cell’s sectorized geometry with windmill sectorization enabled. It is shown by applying a color map that highlights the type of property MATERIAL applied to the different regions resulting from the sectorization.

The methods offered by the subclasses of Cell for setting up the technological geometry only cover the addition and removal of circular regions. The sectorized geometry can be characterized by subdividing the technological geometry into sectors by drawing lines. If a customisation of any of the two available geometry layouts is required, users can make use of the functions in the glow.interface.geom_interface module to build the GEOM face or GEOM compound of need. The methods update_geometry() and update_geometry_from_face() can be used to update either the technological or the sectorized geometry layout with the built GEOM object. This tutorial demonstrates how to customise the cell by updating the sectorized geometry with a GEOM compound containing more circles between two adjacent regions of the technological geometry. Users should note that the previously set sectorization geometry is substituted by the new one. The result of the following code is shown in Fig. 26.

# Setup the XYZ coordinates of the centres of the circles
centres = [(0, 0.1, 0), (0, -0.1, 0), (0.1, 0, 0), (-0.1, 0, 0)]
# Build the corresponding 'Circle' objects, all with the same radius
circles = [Circle(centre, radius=0.05) for centre in centres]
# Build circles positioned in the cell centre
center_circles = [Circle(radius=r) for r in [0.32, 0.34, 0.36, 0.38]]
# Update the list of 'Circle' objects
circles += center_circles

# Partition the original cell's technological geometry with all the circles
updated_face = make_partition(
    [cell.face], [c.face for c in circles], ShapeType.FACE)
# Update the cell's sectorized geometry with the just built shape
cell.update_geometry_from_face(GeometryType.SECTORIZED, updated_face)
# Show the result in the 3D viewer
cell.show(PropertyType.MATERIAL, GeometryType.SECTORIZED)

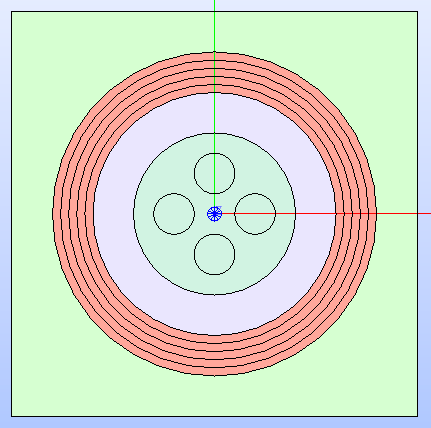
Fig. 26 Cartesian cell’s sectorized geometry after updating it by adding several circles. It is shown by applying a color map that highlights the type of property MATERIAL applied to the different regions resulting from the updated sectorized geometry.

Cartesian Assembly With Symmetry

The use case cartesian_assembly.py shows the steps required to declare an assembly made by a central cell (of cartesian type) around which several rings of the same cell are placed. This type of geometry layout can be tracked by the SALT module of DRAGON5 using an eighth symmetry as this is the minimum portion of the geometry that can describe the entire layout of the assembly.

The first step for assembling this use case geometry is to instantiate the cartesian cell (i.e. object of the class RectCell) which constitutes the lattice. The instructions that follow build a cartesian cell with a square shape whose edge is 1.0 long; the cell is subdivided into four regions by means of three circles and the type of property MATERIAL is assigned to each. In addition, the regions are sectorized with the windmill option enabled.

# Build the cell's geometry layout by adding three circular regions
cell = RectCell(name="Cartesian cell")
radii = [0.2, 0.3, 0.4]
for radius in radii:
      cell.add_circle(radius)
# Assign the materials to each zone in the cell
cell.set_properties(
    {PropertyType.MATERIAL: ["MAT_1", "MAT_2", "MAT_3", "MAT_4"]}
)
# Apply the cell's sectorization
cell.sectorize([1, 1, 4, 8], [0, 0, 0, 22.5], windmill=True)

The subsequent step is to declare the instance of the class Lattice and add the cells it is made of. A single cell is provided when instantiating the lattice; this cell is placed at the centre of the lattice since the cell and the lattice share the same coordinates for their centres. To add several rings of the same cell, the method add_rings_of_cells() is provided with the instance of the RectCell class, previously declared, and the number of rings to add. The lattice’s technological geometry resulting from assembling all the rings of cells is shown in Fig. 27.

# Build the lattice with several rings of the same cartesian cell
lattice = Lattice([cell], 'Cartesian Lattice')
lattice.add_rings_of_cells(cell, 4)
lattice.show(PropertyType.MATERIAL)

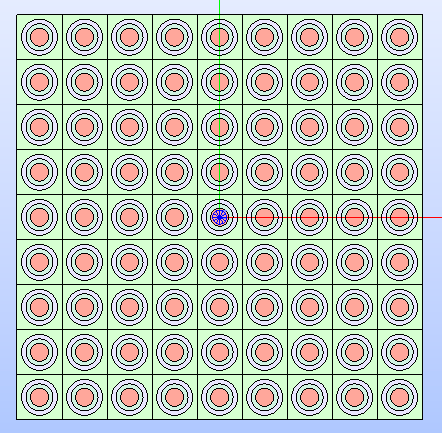
Fig. 27 Cartesian lattice’s technological geometry resulting by adding several rings of cells. It is shown by applying a color map that highlights the type of property MATERIAL applied to the different regions of its cells.

To replicate a fuel assembly, the lattice needs to be framed into a box. This can be performed in different ways in GLOW, either by calling the method build_lattice_box() that automatically builds a rectangular box with layers of the indicated thicknesses or by instantiating a RectCell object and assigning it to the lattice_box property. In the following, the second option is shown. The cell is built from the XY dimensions of the lattice and the thickness of the layers. In this specific use case, the box cuts the GEOM compound of the cells located on the outermost ring, i.e. the cells farthest from the centre of the lattice. In addition, the geometric shape of the box’s single layer is subdivided in rectangular sub-shapes. The lattice’s technological geometry resulting from assembling the box with the lattice is shown in Fig. 28.

# Build the cell representing the lattice's box so that it sligthly cuts
# the outmost ring of cells; the box is subdivided by means of squares at
# its corners. The dimensions of the lattice are extracted to get the box
# dimensions.
x_min, x_max, y_min, y_max = get_bounding_box(lattice.lattice_cmpd)
thickness = 0.1
box = RectCell(
    height_x_width=((y_max-y_min) + thickness, (x_max-x_min) + thickness)
)
box.set_properties({PropertyType.MATERIAL: ["MAT_2"]})
# Build the characteristic shapes that subdivide the box
layer_1 = Rectangle(
    height=(y_max-y_min) - thickness,
    width=(x_max-x_min) - thickness
)
corners = [
    Rectangle((x_max, y_max, 0.0), thickness, thickness),
    Rectangle((x_max, y_min, 0.0), thickness, thickness),
    Rectangle((x_min, y_min, 0.0), thickness, thickness),
    Rectangle((x_min, y_max, 0.0), thickness, thickness),
]
# Assemble all the geometric shapes together
box_face = make_partition(
    [box.face],
    [layer.face for layer in [layer_1] + corners],
    ShapeType.COMPOUND
)
# Update the box cell's technological geometry with the assembled one
box.update_geometry_from_face(GeometryType.TECHNOLOGICAL, box_face)

# Assemble the box's cell with the whole lattice and show the result in the
# SALOME 3D viewer
lattice.lattice_box = box
lattice.show(PropertyType.MATERIAL)

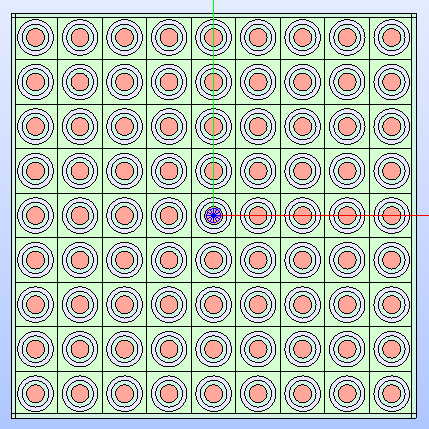
Fig. 28 Cartesian lattice’s technological geometry resulting by framing the cells in a box that sligthly cuts the outmost ring of cells.

A symmetry can be applied to the lattice’s geometry layout. For the specific layout of this use case, the EIGHTH type of symmetry can be used in tracking calculations since it is the minimum portion that can represent the entire geometry layout of the lattice. The result of applying the above mentioned type of symmetry is shown in Fig. 29.

# Apply the eighth symmetry type to the cartesian lattice
lattice.apply_symmetry(SymmetryType.EIGHTH)
# Show the resulting layout with the 'MATERIAL' color map
lattice.show(PropertyType.MATERIAL)

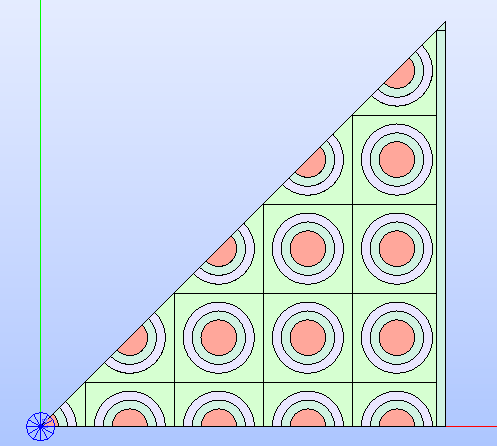
Fig. 29 Cartesian lattice’s technological geometry resulting by framing the cells in a box and applying the EIGHTH type of symmetry.

This geometry layout for the assembly can be exported to the output TDT file by calling the function analyse_and_generate_tdt(). It is possible to indicate which GeometryType of the cells to use in the analysis that GLOW performs to generate the output TDT file. In the following, the instance of the dataclass TdtSetup is provided specifying the SECTORIZED type of geometry. The resulting geometry, which the SALT module of DRAGON5 can perform tracking calculations on, is shown in Fig. 30.

# Perform the geometry analysis and export the TDT file of the surface
# geometry
analyse_and_generate_tdt(
    [lattice], "cartesian_lattice", TdtSetup(GeometryType.SECTORIZED))

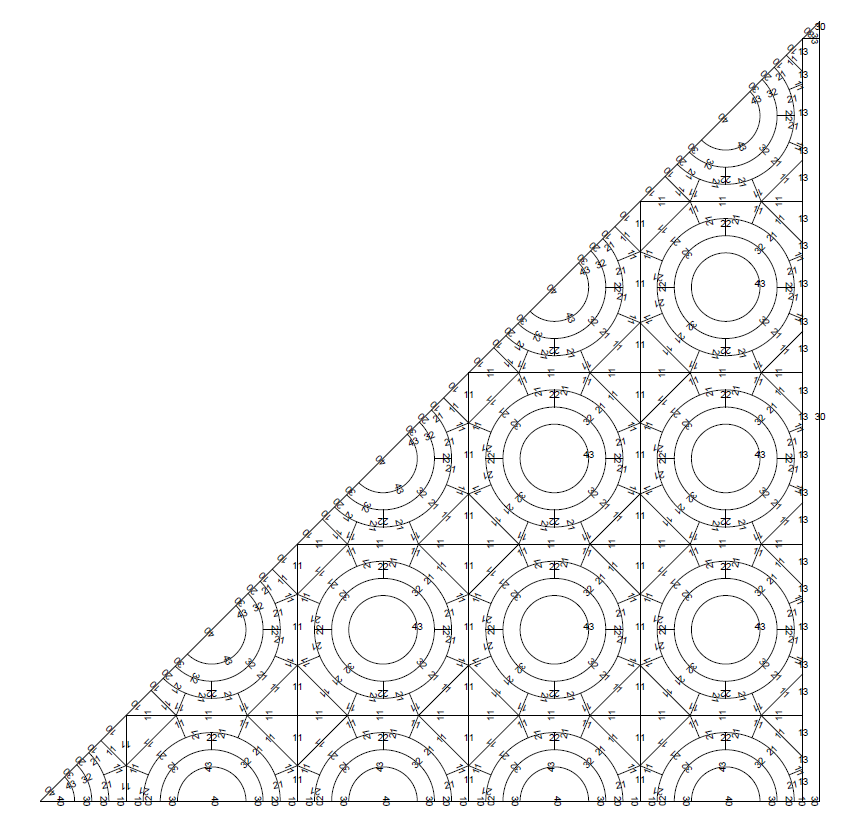
Fig. 30 Cartesian lattice’s geometry layout that the SALT module of DRAGON5 uses to perform the tracking.

Hexagonal Assembly With Different Cells

The use case hexagonal_assembly.py shows the steps required to declare an assembly made by several rings of the same hexagonal cell framed in a hexagonal box. In addition, a hexagonal cell having different dimension, layout and materials combination is positioned at different XYZ coordinates within the lattice.

The first step in assembling the use case geometry is to instantiate the hexagonal cell (i.e. the object of the class HexCell) the lattice is made out of. The two hexagonal cells that characterise the lattice are built with edges 1.0 and 2.0. The former cell, which constitutes the main pattern of the geometry layout, is subdivided into five regions by means of four circles; the latter has a different layout characterized by two circular regions. In addition, the first cell is rotated by 90° so that the final assembly is enclosed in a X-oriented hexagonal box, as requested by the SALT module of DRAGON5. The type of property MATERIAL is assigned to the regions of each cell.

# Build the hexagonal cell that constitutes the lattice. It is rotated
# by 90° as needed for tracking
cell_1 = HexCell(name="Cell 1")
cell_1.rotate(90)
radii = [0.1, 0.6, 0.625, 0.70]
for radius in radii:
    cell_1.add_circle(radius)
cell_1.set_properties(
    {PropertyType.MATERIAL: [
        "GAP", "FUEL", "GAP", "CLADDING", "COOLANT"]}
)
# Build the second hexagonal cell
cell_2 = HexCell(edge_length=2.0, name="Cell 2")
radii = [1.0, 1.25]
for radius in radii:
    cell_2.add_circle(radius)
cell_2.set_properties(
    {PropertyType.MATERIAL: ['COOLANT', 'CLADDING', 'COOLANT']}
)

The subsequent step is to declare the instance of the class Lattice and add the cells it is made of. A single cell (the one with smaller size) is provided when instantiating the lattice. This cell is placed at the centre of the lattice as they both have the same coordinates of the centre. Several rings of the same cell are then added with the method add_rings_of_cells(): the instance of the HexCell class, previously declared, is provided together with the number of rings to add. To complete the lattice’s geometry layout, the cell with greater size is added at specific coordinates using the method add_cell(). The resulting geometry layout (see Fig. 31) shows that larger cells overlap smaller cells because they have been placed in a higher layer. Consequently, the GEOM compound of each cell in the lower layer is cut out of the GEOM compound of the cells in the upper layer.

# Build the lattice with several rings of the same cartesian cell
lattice = Lattice([cell_1])
lattice.add_rings_of_cells(cell_1, 6)
# XY coordinates of the centres of the cells with greater size
x = 4.330127
y = 4.5
lattice.add_cell(cell_2, ())
lattice.add_cell(cell_2, (x, y, 0.0))
lattice.add_cell(cell_2, (-x, y, 0.0))
lattice.add_cell(cell_2, (x, -y, 0.0))
lattice.add_cell(cell_2, (-x, -y, 0.0))
# Show the lattice's technological geometry with the 'MATERIAL' color map
lattice.show(PropertyType.MATERIAL)

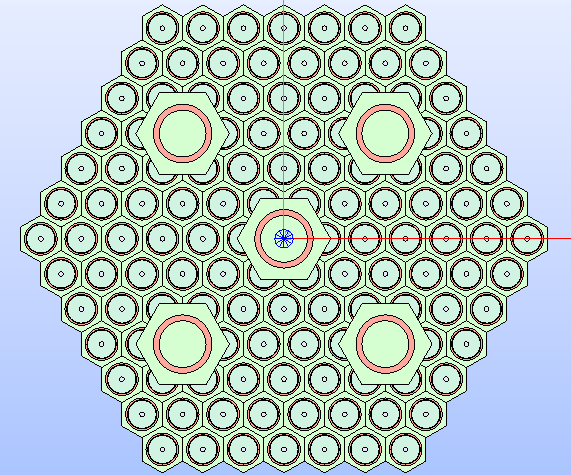
Fig. 31 Hexagonal lattice’s technological geometry resulting by adding several rings of cells with smaller size and cells with a greater size at different coordinates. The resulting geometry layout shows that the cells of the higher layer cut those of the layer below. The color map that highlights the type of property MATERIAL is applied to the different regions of the lattice’s cells.

The current lattice’s geometry layout shown in Fig. 31 presents a situation where the structural parts (e.g. regions associated with a fuel material) of the smaller cells are cut. Since this scenario cannot happen in real-life situations, these cells need to be restored by removing any circular region. This is done by using the function get_changed_cells(), to retrieve the cut cells, and the method restore_cells(), to restore the geometry layout and assign a value for the provided types of property. Fig. 32 shows the result of restoring the cut cells.

# Get the cells whose geometry layout has been cut and restore them by
# assigning a specific property type
lattice.restore_cells(
    get_changed_cells(lattice),
    {PropertyType.MATERIAL: 'COOLANT'}
)

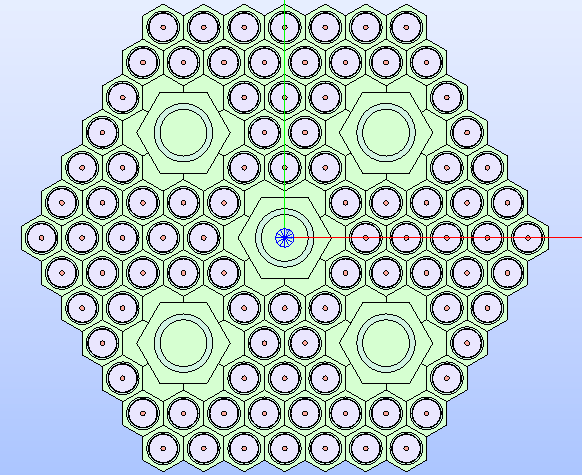
Fig. 32 Hexagonal lattice’s technological geometry resulting by restoring the geometry layout of those cells that have been cut. The color map that highlights the type of property MATERIAL is applied to the different regions of the lattice’s cells.

An assembly requires the lattice to be framed into a box. In this use case the method build_lattice_box() is used. It automatically builds an X-oriented hexagonal box with layers of the indicated thicknesses. The type of property MATERIAL is assigned to the different regions of the hexagonal box by means of the method set_lattice_box_properties() with the values assigned according to the distance of the regions from the centre of the box. The resulting assembly is shown in Fig. 33.

# Add a container for the assembly and assign properties
lattice.build_lattice_box([0.15, 0.15])
lattice.set_lattice_box_properties(
    {PropertyType.MATERIAL: ['COOLANT', 'CLADDING', 'COOLANT']})
# Show the lattice's technological geometry
lattice.show(PropertyType.MATERIAL)

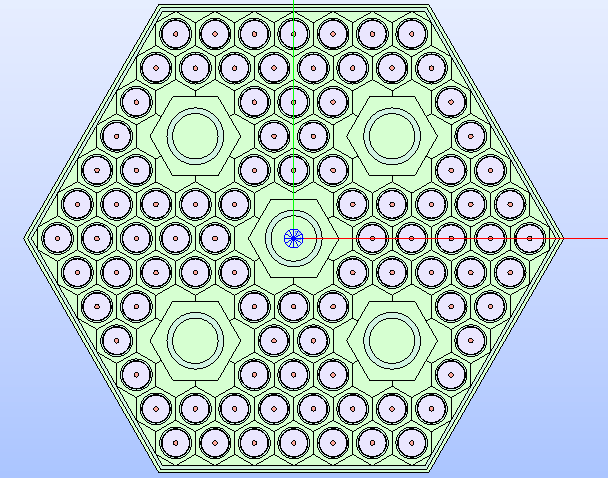
Fig. 33 Hexagonal lattice’s technological geometry resulting by framing the cells into a box.

If the just built geometry layout of the assembly is exported to the output TDT file by calling the function analyse_and_generate_tdt(), the resulting surface representation will be characterised by typgeo=0, which implies a uniform tracking type (i.e. TISO) in the ALBE 1.0 condition for its boundaries. This requirement can be changed by assigning a lattice type of geometry that results in a TRANSLATION BC type applied to the lattice’s boundaries. To do so, the lattice’s property type_geo must be set to HEXAGON_TRAN. This setting generates a surface representation that must be tracked by a cyclic method (i.e. TSPC). After changing the lattice type of geometry, the output TDT file can be generated.

# Change the lattice type of geometry to use 'TRANSLATION' BCs and cycling
# tracking type
lattice.type_geo = LatticeGeometryType.HEXAGON_TRAN
# Perform the geometry analysis and export the TDT file of the surface
# geometry
analyse_and_generate_tdt([lattice], 'hexagonal_assembly')

Colorset

The use case colorset.py shows the steps required to build the S30 portion of a colorset made by two different hexagonal assemblies. The layout of the colorset implies that the control rod assembly is surrounded by six fuel assemblies. In the specific case of this example, given the available symmetry of one twelfth of the colorset (i.e. S30), only the two assemblies that concur in identifying the portion to study are built.

The first step in assembling the use case geometry is building the fuel assembly, which is made by two hexagonal cells (i.e. the object of the class HexCell) with different layout.

The two hexagonal cells that characterise the lattice are built with the same edge of 1.0, but different number of circular regions. The cell which constitutes the main pattern of the geometry layout is subdivided into five regions by means of four circles; the other cell, which is placed in the lattice centre, is characterized by two circular regions. In addition, both cells are rotated by 90° so that the final assembly is enclosed in a X-oriented hexagonal box. The type of property MATERIAL is assigned to the regions of each cell.

# Build the hexagonal cells of the fuel assembly
fuel_cell = HexCell(name="Cartesian cell")
fuel_cell.rotate(90)
radii = [0.2, 0.6, 0.62, 0.68]
for radius in radii:
    fuel_cell.add_circle(radius)
# Assign the materials to each zone in the cell
fuel_cell.set_properties(
      {PropertyType.MATERIAL: ["GAP", "FUEL", "GAP", "CLADDING", "COOLANT"]}
)
central_cell = HexCell(name="Central cell")
central_cell.rotate(90)
for radius in [0.6, 0.65]:
    central_cell.add_circle(radius)
# Assign the materials to each zone in the cell
central_cell.set_properties(
      {PropertyType.MATERIAL: ["GAP", "CLADDING", "COOLANT"]}
)

The fuel assembly is built by instantianting an object of the class Lattice and adding the cells it is made of. The central cell is provided when instantiating the lattice. Several rings of the same cell are then added with the method add_rings_of_cells(): the instance of the HexCell class, previously declared, is provided together with the number of rings to add. To complete the fuel assembly’s geometry layout, the lattice is enclosed in a box which overlaps the last ring of hexagonal cells without cutting the structural parts of those cells (i.e. the circular regions remain untouched). The method build_lattice_box() is used by providing a negative first value in the list of thicknesses. The type of property MATERIAL is assigned to the different regions of the hexagonal box by means of the method set_lattice_box_properties() with the values assigned according to the distance of the regions from the centre of the box. The resulting assembly is shown in Fig. 34.

# Build the fuel assembly lattice of the colorset
fuel_assembly = Lattice([central_cell], "Fuel Assembly")
fuel_assembly.add_rings_of_cells(fuel_cell, 5)
# Build the fuel assembly box
fuel_assembly.build_lattice_box([-0.1, 0.3, 0.3])
fuel_assembly.set_lattice_box_properties(
    {PropertyType.MATERIAL: ["COOLANT", "CLADDING", "COOLANT"]}
)
# Display the fuel assembly with the MATERIAL color map
fuel_assembly.show(PropertyType.MATERIAL)

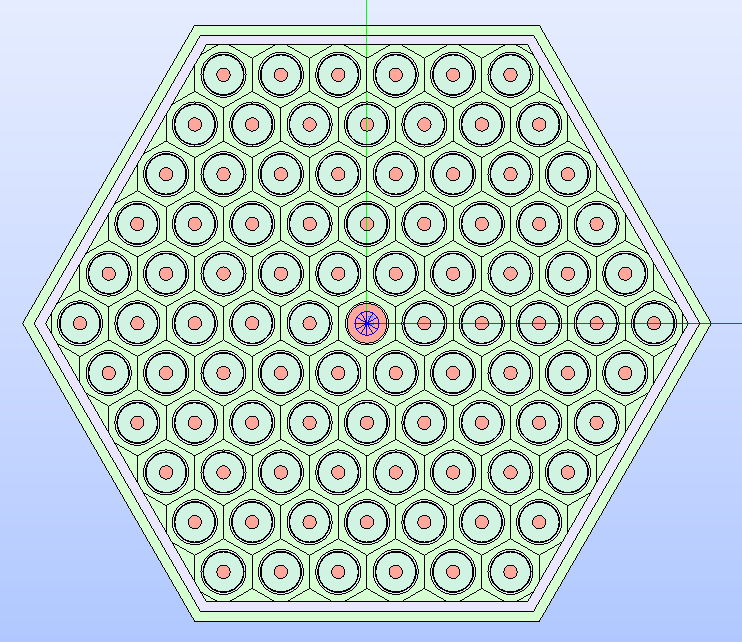
Fig. 34 The fuel assembly’s technological geometry resulting by framing the cells into a box. Regions are displayed according to the MATERIAL color map.

The second step in deriving the colorset layout is building the control rod assembly. Its layout is characterised by control rod pins, modelled as circles, placed within a central circular area. The lattice that replicates this layout is considered to be made of circular cells. Since there is not a pre-defined class for a circular cell, the user can rely on the class GenericCell. This class is meant to describe a cell with any given layout which is different from the typical hexagonal or Cartesian ones. In this sense, given a set of characteristic geometric data, the central cell and the box cell (a HexCell instance) are built.

# Data
pitch = fuel_assembly.lattice_box.figure.ly * 2
edge_bypass = (pitch) / math.sqrt(3)
edge_ext_wrap_o = (pitch - 0.4) / math.sqrt(3)
edge_ext_wrap_i = (pitch - 0.6) / math.sqrt(3)
r_cr_circles_i = 3.2
r_cr_circles_o = 5.2
cr_pin_radii = [0.68, 0.7, 0.78]
cr_wrapper_radii = [7, 7.25]
int_shaft_ir = 1.4
int_shaft_or = 1.7

# Build the central cell of the control rod assembly
cr_cell = HexCell(edge_length=edge_ext_wrap_i, name= "Control Rod cell")
# Add the circles representing the different zones
for r in cr_wrapper_radii:
    cr_cell.add_circle(r)
cr_cell.set_properties(
    {PropertyType.MATERIAL: ["COOLANT", "CR_CLADDING", "CR_MIX"]}
)

To build and properly position the control rod pin cells, two functions are included in the script: the create_vertices_list function produces a list with a given number of vertex objects laying on the same circumference having the given radius. The make_circular_cells_list function creates a list of circular cells, as GenericCell instances, with centers provided by a list of vertex objects.

# Build the vertices at which the control rod cells are placed
cr_vertices_i = create_vertices_list(r_cr_circles_i, 6)
cr_vertices_o = create_vertices_list(r_cr_circles_o, 12)
# Build the circular control rod cells placed along two circumferences
cr_cells_i = make_circular_cells_list(cr_vertices_i, cr_pin_radii)
cr_cells_o = make_circular_cells_list(cr_vertices_o, cr_pin_radii)

Lastly, the shaft cell is built; it is represented by a GenericCell instance made by three concentric circles.

# Build the central shaft cell as made by three concentric circles
circle_shaft_i = Circle(
    radius=int_shaft_ir, name="Inner Shaft Circle"
)
circle_shaft_o = Circle(
    radius=int_shaft_or, name="Outer Shaft Circle"
)
shaft_compound = make_partition(
    [circle_shaft_o.face, circle_shaft_i.face], [], ShapeType.FACE)
set_shape_name(shaft_compound, "Shaft Cell")
shaft_cell = GenericCell(shaft_compound)
shaft_cell.set_properties(
    {PropertyType.MATERIAL: ["COOLANT", "CR_CLADDING"]}
)
# Dummy assignement of the cell's type so that it can be added to a hexagonal
# lattice
shaft_cell.cell_type = CellType.HEX

The fuel assembly is built by instantianting an object of the class Lattice and adding the cells it is made of. In addition, the cell representing the assembly box is assigned to the lattice’s attribute lattice_box. The resulting assembly is shown in Fig. 35.

# Build the control rod assembly
cr_assembly = Lattice([cr_cell], "Control Rod Assembly")
# Add the two rings of rod pin cells to the control rod assembly
for cell in cr_cells_i + cr_cells_o:
    cr_assembly.add_cell(cell, ())
# Add the shaft cell to the control rod assembly
cr_assembly.add_cell(shaft_cell, ())
# Assign the built box cell to the control rod assembly
cr_assembly.lattice_box = box_cell

# Display the control rod assembly
cr_assembly.show(PropertyType.MATERIAL)

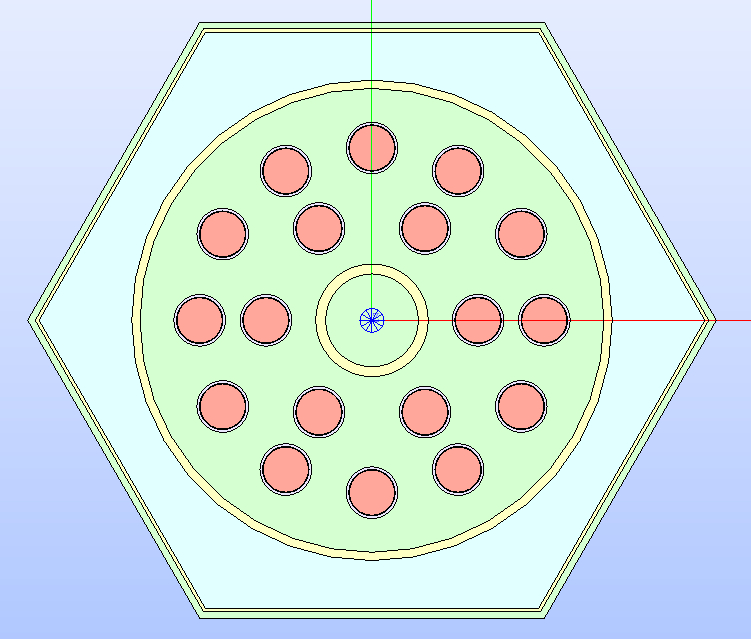
Fig. 35 The control rod assembly’s technological geometry whose regions are displayed according to the MATERIAL color map.

The layout of the S30 colorset to replicate requires that the fuel assembly is translated to the upper-right side of the control rod assembly. The resulting compound made by the two assemblies and the portion identifying the S30 symmetry are built. The latter requires that a common operation between the entire layout and the shape of the symmetry is performed. The resulting GEOM compound object of the colorset portion is added to the SALOME study.

# Translate the fuel assembly to the right of the control rod assembly
fuel_assembly.translate((3/2*cr_assembly.lx, cr_assembly.ly, 0))

# Build the colorset as a list of the two assemblies
colorset = [cr_assembly, fuel_assembly]
# Build the colorset compound and display it in the SALOME 3D viewer
colorset_cmpd = make_compound([lattice.lattice_cmpd for lattice in colorset])

# Extract the S30 symmetry portion out of the entire colorset
edges = build_contiguous_edges(
    [
        make_vertex((0.0, 0.0, 0.0)),
        make_vertex((3/2*fuel_assembly.lx, fuel_assembly.ly, 0.0)),
        make_vertex((2*fuel_assembly.lx, 0.0, 0.0))
    ]
)
cutting_face = make_face(edges)
colorset_portion = make_common(colorset_cmpd, cutting_face)
add_to_study(colorset_portion, "Colorset - S30 Symmetry")

To enable the visualization of the regions of the colorset portion that belong to the two assemblies at once with the same MATERIAL color map, the regions, and the names of the materials, are collected. Given the number of unique materials, colors are generated and associated to the regions. The regions are then added to the SALOME study so that they can be displayed in the 3D viewer of SALOME. The result is show in Fig. 36.

# Display all the regions of the two assemblies by using the same colormap
colorset_regions: List[Region] = []
material_names: List[str] = []
for lattice in colorset:
    for region in lattice.regions:
        if get_min_distance(colorset_portion, region.face) > 1e-6:
            continue
        new_region = make_common(region.face, colorset_portion)
        # Continue with the next region if the common shape does not hold
        # any face, meaning that the region and the portion do not overlap
        if not extract_sub_shapes(make_compound([new_region]),
                                  ShapeType.FACE):
          continue
        # Store the material name, if not present
        mat_name = region.properties.get(PropertyType.MATERIAL)
        if mat_name is None:
            raise RuntimeError(f"No material for region {region}.")
        if mat_name not in material_names:
            material_names.append(mat_name)
        # If the result is a compound or a shell, extract the contained faces
        if get_shape_type(new_region) in [ShapeType.COMPOUND,
                                          ShapeType.SHELL]:
            for new_region in extract_sub_shapes(new_region, ShapeType.FACE):
                colorset_regions.append(
                    Region(
                        new_region,
                        name=region.name,
                        properties=deepcopy(region.properties)
                    )
                )
            continue
        colorset_regions.append(
            Region(
                new_region,
                name=region.name,
                properties=deepcopy(region.properties)
            )
        )

# Generate a specific amount of colors as the number of different
# values for the same given property type
colors = generate_unique_random_colors(len(material_names))
# Join the material names with the colors
materials_vs_color = dict(zip(material_names, colors))

# Display the regions of the colorset portion with the material color map
for region in colorset_regions:
    # Get the color according to the material name of the region
    region.color = materials_vs_color[
        region.properties[PropertyType.MATERIAL]
    ]
    set_color_face(region.face, region.color)
    add_to_study_in_father(colorset_portion, region.face, region.name)

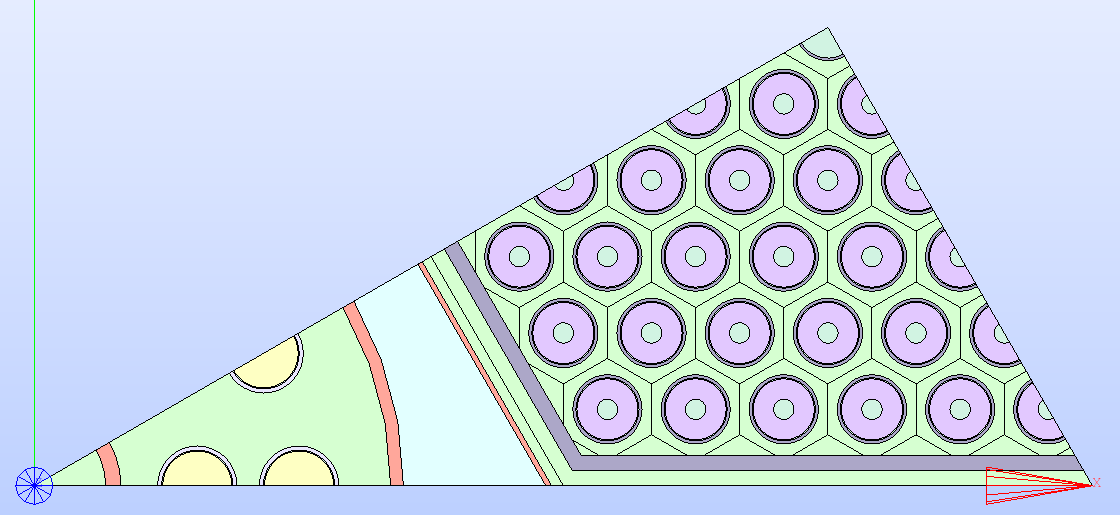
Fig. 36 The technological geometry of the colorset portion replicating the S30 symmetry. Its regions are displayed according to the MATERIAL color map.

Lastly, the surface geometry representation of the colorset portion is exported to an output TDT file by setting the TdTSetup attributes so that the TDT file describes an S30 symmetry for an isotropic tracking (TISO) in the SALT module of DRAGON5. In addition to the list of Lattice objects belonging to the colorset, the GEOM compound representing the S30 symmetry of the colorset is provided. The analysis and export functionalities will generate a TDT file from this indicated layout.

# Generate the TDT file from the colorset portion using a specific typgeo and
# symmetry type
analyse_and_generate_tdt(
    colorset,
    "colorset_s30",
    tdt_config=TdtSetup(
        type_geo=LatticeGeometryType.SYMMETRIES_TWO,
        symmetry_type=SymmetryType.TWELFTH),
    compound_to_export=colorset_portion)